\\int \left( \tan x \cot x \right)^2 \ \ = \int\left( \tan^2 x \cot^2 x 2 \tan x \cot x \right)dx\ \ = \int\left( \tan^2 x \cot^2 x 2 \right)dx\ What I get is let u = sin x then or du = cos x dx So Rather than saying u = sin x, use u = 2x instead Just expand tan u into This integral is much easier to solve Expanding sin 2x and cos 2x in terms of sin x and cos x just makes things more complicatedIntegration If the integral ∫ (5 tan x / tan x − 2)dx = x a ln sin x 2 cos x k, then a is equal to 1 2 2 1 Answer ∫ (5 tan x / tan x 2)dx = ∫ (5 sin x / sin x 2 cos x)dx ∫ 2 (cos x 2 sin x) (sin x 2 cos x) / (sin x 2 cos x)dx
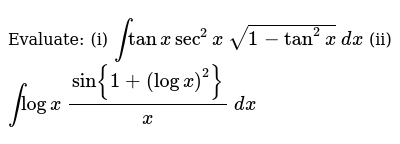
Evaluate I Inttanxsec 2x Sqrt 1 Tan 2x Dx Ii Intlogx Sin 1 Logx 2 X Dx
